Линейная интерполяция в Unity

Содержание

Что такое Lerp
Определение интерполяции
Формула интерполяции
Lerp в Unity
Варианты интерполяции
Виды интерполяции
Пример использования Lerp для перемещения объекта
Пример не самого удачного использования Lerp
Как использовать Lerp с Vector3
Как использовать Lerp с Curve
Как использовать Lerp с поворотами
Как использовать Lerp с масштабированием
Как использовать Lerp для изменения цвета
Как сделать Fade-эффект
Как сделать Fade-эффект текста
Как создать Fade-эффект для аудио
Выводы

Очень часто, используя Unity, нам требуется анимировать кнопки, создавать передвижения объектов к новой позиции, плавно приглушать аудио, изменять цвет объекта через какие-либо промежутки времени.

Для всех этих задач очень хорошо подходит функция Lerp — Линейная интерполяция.

Что такое Lerp

Определение интерполяции

Интерполяция — способ нахождения промежуточных значений. Она применяется для плавного изменения какого-либо параметра от одного значения до другого, например, положения объекта.

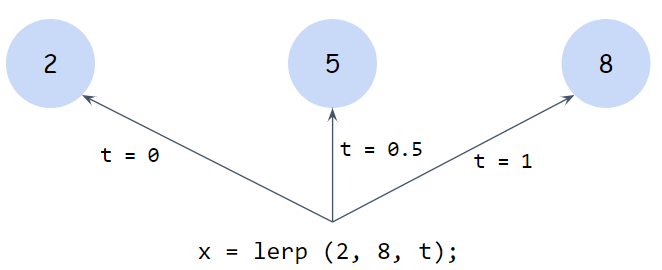
Суть интерполяции состоит в следующем. В функцию передается два параметра («2» и «8») и затем параметр t. Если t равен 0, то функция возвращает значение первого параметра (2), если t = 1, то второго (8). Если параметр t равен 0.5, то функция вернет значение ровно посередине между 2 и 8, то есть 5. Таким образом, за счет параметра t, происходит плавное изменение от одного значения параметра к другому.

Условно, мы можем приращивать величину t на бесконечно малое число и получать в результате величину (линейно), которой будет соответствовать данная t между числами (2) и (8).

Формула интерполяции

Сама линейная интерполяция реализует следующую формулу:

С = A * (1 — t) + B * t, где

С — величина интерполяции
A — начальное число
B — конечное число
t — шаг интерполяции (дельта), равный от 0 до 1

Lerp в Unity

К счастью нам не требуется использовать данную формулу и вычислять значения вручную, т.к. в Unity данные вычисления реализованы в виде метода:

Lerp(firstNumber, secondNumber, delta).

Рассмотрим небольшой пример. Мы хотим вычислить середину отрезка, с начальной координатой 0 и конечной координатой 100.

Реализация метода Lerp в этом случае будет выглядеть следующим образом:

float _firstPoint = 0;
float _secondPoint = 100;
float _delta = 0.5f;

var lerpResult = Mathf.Lerp(_firstPoint, _secondPoint, _delta);

Debug.Log(lerpResult.ToString()); // Выведет 50 в консоль

Варианты интерполяции

Интерполировать можно не только числа. Также можно интерполировать Vector3, Color и Кватернионы:

var r_f = Mathf.Lerp(a_f, b_f, t);
var r_v = Vector3.Lerp(a_v, b_v, t);
var r_c = Color.Lerp(a_c, b_c, t);
var r_q = Quaternion.Lerp(a_q, b_q, t);

Виды интерполяции

Линейная интерполяция нужна для плавного перемещения объекта по прямой.

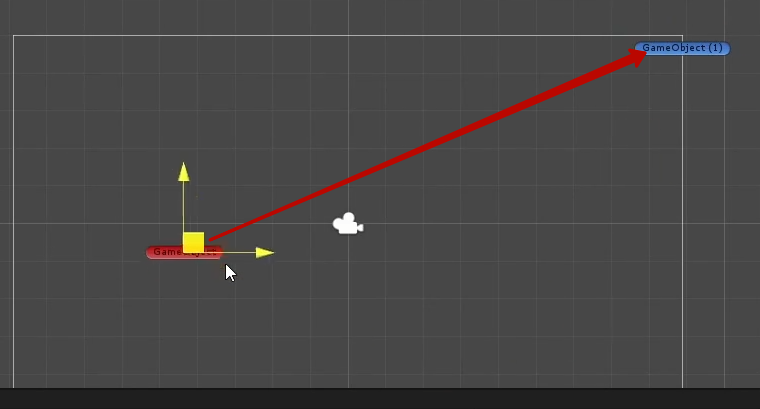
Есть еще Slerp — это интерполяция движения объекта по окружности. В контексте данной статьи мы этот метод рассматривать не будем.

Есть еще прямая интерполяция — MoveTowards. При этом объект будет двигаться плавно, но с одинаковой скоростью — по прямой.

Пример использования Lerp для перемещения объекта

Самое распространенное использование Lerp — это выполнение перемещения одного объекта к другому за определенное фиксированное время.

Как корректно использовать Lerp?

Создать таймер, который будет инкрементироваться каждый фрейм
Разделить оставшееся время на величину времени движения объекта
Использовать данную величину, как дельту интерполяции

В следующем примере расположим на сцене зеленый квадрат и красный прямоугольник.

Напишем скрипт следующего содержания:

[SerializeField] private Transform _goalObject;

private float _timeForMoving = 4;
private float _elapsedTime;
private Vector2 _startPosition;

private void Start() => _startPosition = transform.position;

private void Update()
{
	if ( _elapsedTime < _timeForMoving)
    {
	    float delta = _elapsedTime / _timeForMoving;
        transform.position = Vector2.Lerp(_startPosition, _goalObject.position, delta);
        _elapsedTime += Time.deltaTime;
	}
}

В итоге, мы получаем следующий результат:

Передвижение объекта с помощью Lerp — Зеленый круг двигается дергано, т.к. используется gif-анимация. В реальности движение — плавное

Наша задача — обеспечить передвижение зеленого круга к красному квадрату ровно за 4 секунды.

Для ее решения, в данном скрипте мы приращиваем понемногу значение переменной elapsedTime. Когда мы делим ее на время, которые мы выделили для перемещения (равное 4 секунды), то получаем линейную величину координаты, в которой должен оказаться объект за данное время.

Другими словами:

за 0 секунд — объект должен оказаться в точке A (исходная точка, где находился зеленый круг);
за 4 секунды — объект должен оказаться в точке B (где находится красный квадрат);
за x секунд — объект должен оказаться в точке C, где-то между A и B, которая вычисляется по формуле интерполяции при движении объекта с одинаковой скоростью;

Почему мы вообще используем Time.DeltaTime в данном методе? Ведь можно приращивать просто постоянную величину к переменной elapsedTime.

Мы используем deltaTime, для того чтобы обеспечить точную зависимость пройденного расстояния от частоты кадров. Допустим, возьмем две машины, на которых запущена игра. На одной FPS 100 кадров в секунду, на другой FPS 10 кадров в секунду. Если использовать одинаковую дельту и не использовать deltaTime, то объект на данных машинах переместится за разное реальное время, т.к. в одном случае метод выполнится 100 раз за секунду, во втором случае — 10 раз за секунду. И за 1 секунду времени на первой машине объект условно пройдет расстояние 100 метров, на второй машине — 10 метров.

Итак, вернемся к Lerp’у. Данный метод не является не самым точным способом передвижения. Т.к. приращивание координат происходит на довольно мелкие величины — конечной координатой может быть точка не с координатой 100, а с координатой 99.9998.

Чтобы избавиться от данной проблемы, можно на самом последнем шаге чуть чуть еще подвинуть объект, присвоив ему координату конечного объекта:

if ( _elapsedTime < _timeForMoving)
{
	float delta = _elapsedTime / _timeForMoving;
    transform.position = Vector2.Lerp(_startPosition, _goalObject.position, delta);
    _elapsedTime += Time.deltaTime;
}
else
{
	transform.position = _goalObject.position;
}

Также Lerp можно спокойно использовать с корутинами. В следующем примере мы вызываем движение зеленого круга к квадрату, при нажатии Enter. При этом повторное нажатие и повторный вызов движения будет происходить только после того, как прошлое передвижение закончится.

[SerializeField] private Transform _goalObject;

private float _timeForMoving = 4;    
private Vector2 _startPosition;
private bool _isMoving;   
    
void Start() => _startPosition = transform.position;

void Update()
{
	if (Input.GetKeyDown(KeyCode.Space) && _isMoving == false)
	    StartCoroutine(LerpCoroutine());
}

IEnumerator LerpCoroutine()
{
	float elapsedTime = 0;
    float delta = 0;
    _isMoving = true;

    while (elapsedTime < _timeForMoving)
    {
	    delta = elapsedTime / _timeForMoving;
        transform.position = Vector2.Lerp(_startPosition, _goalObject.position, delta);
        elapsedTime += Time.deltaTime;
        yield return null;
    }

    transform.position = _goalObject.position;
    _isMoving = false;
}

Пример не самого удачного использования Lerp

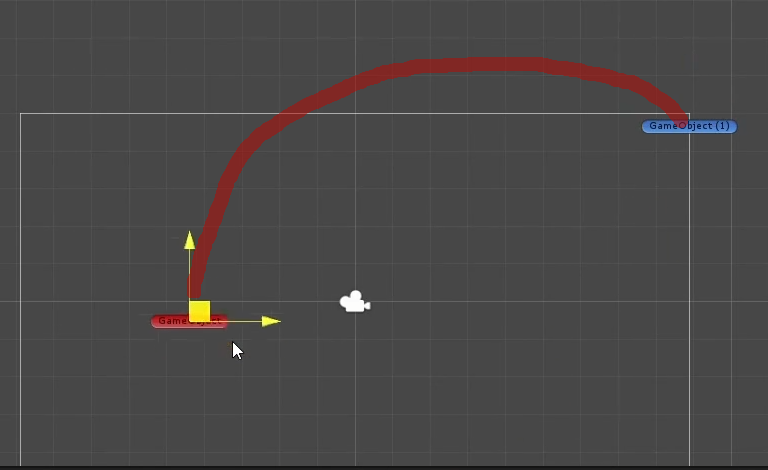
С помощью Lerp можно получить эффект движения одного объекта к другому с плавным замедлением в конце.

Например, так:

Почему данное использование считается не совсем удачным?

Потому что — это уже не линейная интерполяция. Суть линейной интерполяции — это приращение координаты линейно, т.е. одинаковыми промежутками. На данном же примере — объект в самом начале разгоняется, а в конце начинает замедляться. Т.е. тут теряется сама суть линейности.

Плюс ко всему, при таком использовании метода Lerp — он уже не зависит от времени, а начинает зависеть от скорости. Движение объекта происходит со скоростью обратно экспоненциальной оставшемуся расстоянию между объектами.

Сам скрипт выглядит так:

// Трансформа квадрата
[SerializeField] private Transform _squareTransform;

// Вектора для наглядности (см. ниже по тексту)
[SerializeField] private Vector2 _firstVector;
[SerializeField] private Vector2 _secondVector;
[SerializeField] private Vector2 _resultVector;

[Range(0f, 1f)]
[SerializeField] private float _delta;

// Счетчик кадров
private int _frameCounter;

// Выводим начальные координаты круга и квадрата
private void Start()
{
	Debug.Log($"Circle position: {transform.position}");   
    Debug.Log($"Square position: {_squareTransform.position}");
}

private void Update()
{
	_frameCounter++;

    // Делаем действия только для первых трех кадров
    if (_frameCounter < 4)
    {
    // Выводим позицию круга до интерполяции и сдвига
    Vector2 previousPosition = transform.position;
    Debug.Log($"{_frameCounter} ----------------------------------------");
    Debug.Log($"Position before interpolation: {previousPosition}");

    // Производим интерполяцию, двигаем объект и выводим величины:
    // delta и текущая (сдвинутая) позиция объекта
    float delta = Time.deltaTime;
    transform.position = Vector2.Lerp(transform.position, _squareTransform.position, delta);
    Debug.Log($"Time.DeltaTime: {delta}");
    Debug.Log($"Position after interpolation: {transform.position}");
    }

    // Это для наглядности (см. ниже по тексту)
    _resultVector = Vector2.Lerp(_firstVector, _secondVector, _delta);
}

Основная фишка такого использования — это то, что мы на каждом шаге используем в качестве точки A — текущую позицию круга.

transform.position = Vector2.Lerp(transform.position, _squareTransform.position, delta);

Соответственно расстояние становится всё меньше и величина, полученная методом Lerp становится также всё меньше (500 / 0.1 = 5 000 vs 50 / 0.1 = 500). Координата объекта круга приращивается на всё меньшее значение — объект замедляется.

Рассмотрим данный пример на конкретных цифрах:

Запускаем наше приложение и начинаем считать вручную (для простоты я буду считать только одну координату X, т.к. для Y всё остается тем же самым, по тем же правилам):

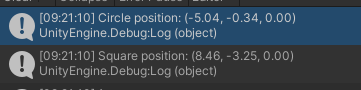
Начальная позиция круга была: -5.04, квадрата: 8.46.

Расстояние между данными объектами = |-5.04| + |8.46| = 13.5 метров.

Соответственно, что должно происходить в результате интерполяции? Весь этот отрезок, длиной 13.5 метров, делится на равнозначные мелкие отрезки. При интерполяции, когда дельта = 0, то конечная величина также будет равна 0. Когда дельта = 1, то конечная величина равна 13.5 метров.

Значит, если мы поделим отрезок по дельте, равной 0.01, то получится, что каждую 0.01 секунду времени объект должен проходить расстояние (13.5 * 0.01) = 0.135 метра.
И, по идее, за 1 секунду объект пройдет расстояние 13.5 метров.

Смотрим первый шаг:

Дельта у нас получилась равной 0.02. Значит за данное время объект должен пройти расстояние (13.5 * 0.02) = 0.27 метра.

Проверяем: -5.04 + 0.27 = -4.77

Также можно проверить на механизме скрипта, он показывает ту же цифру:

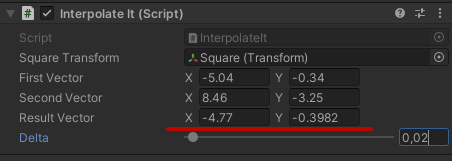
Теперь круг сдвинут и новая координата у него составляет: — 4.77 по оси X.

При этом расстояние до конечного объекта также поменялось. Теперь оно составляет: |-4.77| + |8.46| = 13.23 метров.

Значит, при делении этого отрезка по дельте 0.01 (как выше), расстояние в данную единицу времени уже должно быть: (13.23 * 0.01) = 0.1323 (т.е. объект начинает потихоньку замедляться).

Смотрим второй шаг:

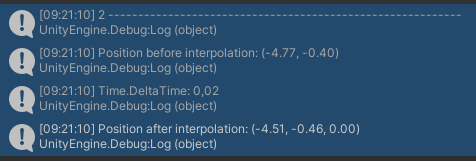
Дельта опять получилась равной 0.02. Значит объект должен пройти расстояние: (13.23 * 0.02) = 0.2646 метра

Проверяем: -4.77 + 0.2646 = -4.51 (примерно)

Третий шаг:

Дельта получилась довольно большой, равной 0.3(3).

Расстояние между кругом и квадратом уже равно: |-4.51| + |8.46| = 12.97 метров. Если опять поделить на дельту 0.01, то получим: (12.97 * 0.01) = 0.1297 (т.е. объект еще больше начинает замедляться)

Для данной дельты объект должен пройти расстояние: (12.97 * 0.3) = 4.32 метра

Проверяем: -4.51 + 4.32 = -0.18

Данный пример, хоть и противоречит «линейности», но вполне может быть использован, например, для плавного движения камеры следом за игровым объектом. Когда в самом начале камера двигается быстро, но в конце начинает плавно замедляться.

Однако, для данного кейса гораздо лучше подходит метод SmoothDamp, который специально предназначен для этой цели и имеет более плавное движение, чем Lerp (отсюда и его название).

Если же мы хотим перемещать объект с фиксированной скоростью, независимо от времени, то для этих целей можно использовать MoveTowards

Как использовать Lerp с Vector3

На самом деле разницы между использованием Lerp с Vector2 и Vector3 — никакой нет. В примерах выше можно заменить Vector2 на Vector3 и всё будет также прекрасно работать.

Как использовать Lerp с Curve

Для того чтобы создать интересный эффект движения можно либо заниматься ручными расчетами, либо сделать проще и использовать компонент Curve.

Например, мы хотим создать эффект, когда объект, движется к целевому объекту, достигает его, откатывается назад, а потом снова возвращается к целевому объекту и двигается обратно.

Для этого напишем следующий скрипт:

[SerializeField] private AnimationCurve _curve;
[SerializeField] private Transform _goalObject;
[SerializeField] private float _timeToMove = 4f;

private void Update()
{
	if (Input.GetKeyDown(KeyCode.Space))
	    StartCoroutine(LerpMove());                
}

IEnumerator LerpMove()
{
	Vector2 startPosition = transform.position;
    Vector2 goalPosition = _goalObject.position;
    // Двигаем объект к целевому положению
    yield return StartCoroutine(Move(startPosition, goalPosition, _timeToMove));

    // Меняем местами начало и конец
    (startPosition, goalPosition) = (goalPosition, startPosition);

	// Двигаем объект обратно
    yield return StartCoroutine(Move(startPosition, goalPosition, _timeToMove));
}

IEnumerator Move(Vector2 startPosition, Vector2 goalPosition, float duration)
{
	float elapsedTime = 0;

    while (elapsedTime < duration)
    {
	    float delta = elapsedTime / duration;
        transform.position = Vector2.Lerp(startPosition, goalPosition, _curve.Evaluate(delta));
        elapsedTime += Time.deltaTime;
        yield return null;
	}

    transform.position = goalPosition;
}

Настроим объект Curve следующим образом:

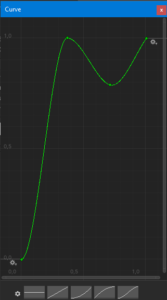
Ключевым моментом в данном скрипте является использование метода: Curve.Evaluate(). Для каждой рассчитанной дельты мы получаем значение Curve. Если подставить его в формулу, то мы будем получать для каждой дельты (растущей от 0 до 1), положение на графике в объекте Curve.

Т.е. фактически мы говорим Юнити: вот сейчас для текущей дельты, на графике Curve значение 0.8. Подставь-ка нам объект туда, где он должен был находиться при дельте, равной 0.8, если бы он двигался линейно.

Поэтому, т.к. на графике мы меняем положение дальше от 1 до 0.8 (примерно), объект возвращается обратно.

Как использовать Lerp с поворотами

Lerp очень хорошо подходит для решения задачи, когда нужно повернуть один объект на определенный угол за конкретное время.

Напишем скрипт, в котором будет происходить поворот объекта на 90 градусов. После чего программа будет ждать 1 секунду и поворачивать объект обратно в нулевую позицию.

[SerializeField] private float _timeToTurn = 1.5f; // время для поворота

private float _elapsedTime; // счетчик прошедшего времени

private void Update()
{
	if (Input.GetKeyDown(KeyCode.Space))
	    StartCoroutine(LerpCoroutine());
}

IEnumerator LerpCoroutine()
{
	// Сперва повернем объект на 90 градусов вокруг z-оси
	Quaternion _targetRotation = Quaternion.Euler(0f, 0f, -90f); 
    yield return StartCoroutine(RotationCoroutine(transform.rotation, _targetRotation, _timeToTurn));

    // Вернемся в стартовую позицию
    _elapsedTime = 0;
    _targetRotation = Quaternion.Euler(Vector3.zero); 
    yield return StartCoroutine(RotationCoroutine(transform.rotation, _targetRotation, _timeToTurn));
}

IEnumerator RotationCoroutine(Quaternion startRotation, Quaternion targetRotation, float rotationTime)
{
	_elapsedTime = 0;
        
    while (_elapsedTime < rotationTime)
    {
	    transform.rotation = Quaternion.Lerp(startRotation, targetRotation, _elapsedTime / rotationTime);
        _elapsedTime += Time.deltaTime;
        yield return null;
	}
        
    // Чуть-чуть подкорректируем rotation в конце
    // из-за неточности Lerp'а
    transform.rotation = targetRotation;
    yield return new WaitForSeconds(1);
}

В данном скрипте мы используем Lerp с кватернионами и, как видим, это прекрасно работает.

Если уйти от корутин и вообще от смысла скрипта, то в общем и целом Lerp с кватернионами работает следующим образом:

Quaternion.Lerp(Quaternion a, Quaternion b, float t);

Т.е. равнозначно перемещению объекта, только в данном случае мы работаем с его поворотами.

Как использовать Lerp с масштабированием

Для масштабирования лучше всего подойдет способ промежуточного вычисления масштаба объекта и присваивания данного масштаба к свойству localScale у transform’ы объекта.

Для этого напишем следующий скрипт:

[SerializeField] private float _timeToScale = 0.5f;

private Vector3 _savedLocalScale;

private void Update()
{
	if (Input.GetKeyDown(KeyCode.Space))
	    StartCoroutine(LerpCoroutine());
}

IEnumerator LerpCoroutine()
{
	float originalScale = 1f;
    float howMuchTimesScale = 2f; // увеличим в 2 раза

    _savedLocalScale = transform.localScale;
    
    // сперва увеличим в 2 раза объект
    yield return StartCoroutine(ScaleCoroutine(originalScale, howMuchTimesScale, _timeToScale));

	// затем уменьшим его до оригинального масштаба
    yield return StartCoroutine(ScaleCoroutine(howMuchTimesScale, originalScale, _timeToScale));
}

IEnumerator ScaleCoroutine(float startValue, float endValue, float scaleTime)
{
	float elapsedTime = 0;
    Vector3 startScale = _savedLocalScale;
    float scaleModifier;

    while (elapsedTime < scaleTime)
    {
	    scaleModifier = Mathf.Lerp(startValue, endValue, elapsedTime / scaleTime);            
        transform.localScale = startScale * scaleModifier;
        elapsedTime += Time.deltaTime;
        yield return null;
	}

    transform.localScale = startScale * endValue;
    yield return new WaitForSeconds(1);
}

В данном примере, с помощью Lerp, мы вычисляем не конечный масштаб, а дельту модификации масштаба.

При увеличении объекта у нас дельта будет постепенно меняться:

1 — 1.1 — 1.2 — 1.3 — 1.4 … 2.

При уменьшении объекта, наоборот: 2 — 1.9 — 1.8 — 1.7 … 1

Всё дело здесь в строке:

transform.localScale = startScale * scaleModifier;

В первом случае, startScale равен первоначальному масштабу трансформы объекта (в нашем примере единица). Поэтому при умножении на дельту, масштаб будет также постепенно расти: 1 — 1.1 — 1.2 — 1.3 — 1.4 … 2.

Во втором случае, мы приравниваем startScale сохраненному первоначальному масштабу трансформы объекта. И при умножении на дельту, масштаб будет уменьшаться от 2 до 1 (2 — 1.9 — 1.8 — 1.7 … 1). И, так как объект после первой итерации был с масштабом 2, то мы от данного масштаба и начинаем его уменьшать, до той степени, пока объект не станет с масштабом — 1.

Как использовать Lerp для изменения цвета

Для того чтобы менять цвет объекта, воспользуемся методом Color.Lerp() и получим следующий результат:

В данном примере квадрат меняет свой цвет с красного на светло-оранжевый.

Скрипт несколько поход на предыдущий, но немного отличается:

[SerializeField] private float _timeToScale = 0.2f;
[SerializeField] private Color _targetColor;

private SpriteRenderer _spriteRenderer;

private void Start() => _spriteRenderer = GetComponent<SpriteRenderer>();

private void Update()
{
	if (Input.GetKeyDown(KeyCode.Space))
	    StartCoroutine(LerpCoroutine());
}

IEnumerator LerpCoroutine()
{
	// Сохраняем оригинальный цвет
	Color savedColor = _spriteRenderer.color;

	// Меняем цвет объекта
    yield return StartCoroutine(ColorCoroutine(_targetColor, _timeToScale));

    // Возвращаемся к оригинальному цвету
    yield return StartCoroutine(ColorCoroutine(savedColor, _timeToScale));
}

IEnumerator ColorCoroutine(Color targetColor, float scaleTime)
{
	float elapsedTime = 0;
    Color startColor = _spriteRenderer.color;
        
    while (elapsedTime < scaleTime)
    {
	    _spriteRenderer.color = Color.Lerp(startColor, targetColor, elapsedTime / scaleTime);
        elapsedTime += Time.deltaTime;
        yield return null;
    }

    _spriteRenderer.color = targetColor;
    yield return new WaitForSeconds(1);
}

В данном случае мы не высчитываем различные коэффициенты, а пользуемся, очень удобно предоставленным нам от Unity, методом Color.Lerp(), в котором достаточно только указать начальный цвет, конечный цвет и дельту — дальше движок всё сделает сам.

В первой корутине мы идём от оригинального цвета к таргет цвету. Во второй, от таргет цвета к оригинальному цвету.

Как сделать Fade-эффект

Fade — это эффект, когда изображение постепенно появляется из темноты (либо наоборот затемняется).

Для создания такого эффекта также очень хорошо подходит Lerp.

Воспользуемся следующим скриптом:

private CanvasRenderer _canvasRenderer;
private float _duration = 3;

private void Start() => _canvasRenderer = GetComponent<CanvasRenderer>();

void Update()
{
	if (Input.GetKeyDown(KeyCode.Space))
	    StartCoroutine(SetAlfa());
}

IEnumerator SetAlfa()
{
	float elapsedTime = 0;
    float startValue = _canvasRenderer.GetAlpha();

    while (elapsedTime < _duration)
    {
	    _canvasRenderer.SetAlpha(Mathf.Lerp(startValue, 0, elapsedTime / _duration));
        elapsedTime += Time.deltaTime;
        yield return null;
    }

    _canvasRenderer.SetAlpha(0);
}

В данном скрипте мы меняем постепенно альфа-канал у компонента Image, расположенного на сцене:

Данное изображение расположено поверх всех остальных объектов, закрывая их. Когда мы меняем прозрачность, то изображение постепенно исчезает и появляются остальные элементы на сцене.

Как сделать Fade-эффект текста

Таким же образом мы можем создать эффект плавного появления и исчезновения текста на сцене.

Для этого также можно воспользоваться компонентом CanvasRenderer и его свойством прозрачности. Напишем следующий скрипт:

[SerializeField] private CanvasRenderer[] _letters;
// Продолжительность фэйда для показа буквы
[SerializeField] private float _durationToShow;
// Продолжительность фэйда для скрытия буквы
[SerializeField] private float _durationToFade;

private void Start()
{
	// Скрываем все буквы на сцене
	foreach (var letter in _letters)	    
	    letter.SetAlpha(0);        
}

void Update()
{
	if (Input.GetKeyDown(KeyCode.Space)) 
	    StartCoroutine(FadeLetter());                       
}

IEnumerator FadeLetter()
{
	// Показываем буквы по одной. Не показываем следуюущую 
	// букву, пока не отрисуется предыдущая.
	foreach(var letter in _letters)    
	    yield return StartCoroutine(SetAlfa(letter, letter.GetAlpha(), 1, _durationToShow));	

    // Скрываем все буквы сразу.
    foreach (var letter in _letters)
        StartCoroutine(SetAlfa(letter, letter.GetAlpha(), 0, _durationToFade));
}

IEnumerator SetAlfa(CanvasRenderer letter, float startValue, float endValue, float duration)
{
	float elapsedTime = 0;        

    while (elapsedTime < duration)
    {
	    letter.SetAlpha(Mathf.Lerp(startValue, endValue, elapsedTime / duration));            
        elapsedTime += Time.deltaTime;
        yield return null;
    }

    letter.SetAlpha(endValue);
}

Суть скрипта довольно простая:

Собираем все CanvasRenderer’ы у букв в массив
Перебираем массив и сперва показываем буквы по одной
Опять перебираем массив и для каждой буквы вызываем корутину скрытия. Тем самым они все запустятся одновременно и будет эффект исчезания всего текста.

Как создать Fade-эффект для аудио

Естественно, Lerp можно использовать для эффекта Fade еще и применительно к аудио. Например, сделать музыку при старте сцены, которая постепенно прибавляет громкость.

Делается это простым скриптом:

[SerializeField] private float _targetValue = 0.8f;
[SerializeField] private AudioSource _audioSource;
[SerializeField] private float _fadeDuration = 10f;
    
void Start() => StartCoroutine(LerpAudio(_audioSource.volume, _targetValue, _fadeDuration));

IEnumerator LerpAudio(float startValue, float endValue, float duration)
{
	float elapsedTime = 0;

    while (elapsedTime < duration)
    {
	    _audioSource.volume = Mathf.Lerp(startValue, endValue, elapsedTime / duration);
        elapsedTime += Time.deltaTime;
        yield return null;
    }

    _audioSource.volume = endValue;
}

Выводы

Итак, настало время подвести выводы.

В большинстве источников говорится о том, что Lerp — это метод, который помогает нам создавать плавное движение объекта на сцене.

Это, в принципе, верное утверждение. Каждый кадр у нас есть определенное расстояние между двумя объектами. Также у нас есть время, которое прошло с момента прошлого кадра. Мы получаем величину отрезка, на который необходимо сдвинуть объект, ориентируясь на время, прошедшее с прошлого кадра. Т.к. время отрисовки каждого кадра разное, то и расстояние, которое проходит объект также и будет разным, но привязанным ко времени отрисовки кадров. Тем самым будет обеспечено плавное (относительно) движение объекта по сцене.

Однако, плавное движение объекта будет обеспечено только если на сцене высокий FPS. Т.к. величина приращения координат объекта экспоненциальна времени, прошедшему от отрисовки прошлого кадра. Получается, чем больше у нас величина Time.deltaTime, тем большее расстояние высчитывается для передвижения объекта и тем более дерганым будет само перемещение. Т.е. если у нас будет машина со слабым FPS, то движение объекта будет происходить дергаными шагами (каждый кадр объект будет перемещаться на большое расстояние и выглядеть это будет, как прыжки с точку в точку), однако, прохождение расстояния всё равно будет примерно одинаковыми отрезками, в случае если FPS остается относительно постоянным.

В чем же различие между Lerp и обычным движением объекта?

Особой разницы между Lerp’ом и обычным движением объекта, через Translate — глобально нет (если использовать Time.deltaTime). Для плавности движения вообще лучше использовать метод SmoothDamp() (либо через Tween’ы — об этом я буду писать в других статьях).

Однако, Lerp вполне можно использовать в следующих вариантах:

Когда нужно обеспечить достижение целевой точки за определенное количество времени, например за 3 секунды.
Когда нужен эффект ускорения в начале и постепенного замедления в конце.
Когда нужно интерполировать движение объекта по кривой (используя Lerp вместе с компонентом Curve)
Кроме движения можно интерполировать кватернионы (т.е. повороты объекта), цвет и материал. Например, можно сделать эффект «исчезающей» фигуры
Можно сделать красивый эффект движения камеры за игроком, когда камера быстро движется за игроком, но замедляется в конце, если игрок встал.
Сделать плавный эффект увеличения масштаба объекта
Сделать, чтобы объект находился точно на определенном расстоянии от другого объекта, даже при изменении расположения целевого объекта в сцене (второй объект будет подтягиваться на это же расстояние)

Возможно я что-либо не учитываю, так как я все-таки начинающий разработчик. Поэтому буду рад, если вы поделитесь своими мыслями и выводами в комментариях.

P.S. Все исходники к данной статье (одним целым проектом в Unity) выложены в данном репозитории